Естествените езици не могат да бъдат използвани за описване на алгоритми, заради възможност от неясно и двусмислено изразяване.
Описаният на естествен език алгоритъм може да се окаже недетерминиран. Средства за недвусмислено представяне на алгоритмите са единствено машинните езици и езиците за програмиране, но програмирането не е умение, което се постига лесно.
—В следващи
уроци ще се учим да представяме алгоритмите
на езика за програмиране C#.
Описване на алгоритми – чрез ограничен естествен език
—Вдясно е представена, на ограничен
естествен
език, процедура за решаване
на линейното уравнение
a.x +
b = 0.
Да изпълним
процедурата, като зададем
за
променливата a
стойност –7, а за
променливата b
– стойност 14. На стъпка 3, в
променливата x
се пресмята –b/а =
–14/–7 = 2 и процедурата ще изведе 2. Забележете различното
значение, което влагаме в знака за равенство при описанието
на алгоритмични процедури – пресмята
се изразът, който е отдясно на знака и стойността
му е новата стойност на променливата отляво. Казваме, че
пресметнатата стойност на израза
се
присвоява на променливата.
—Ако
се опитаме да изпълним тази процедура с коя да е
стойност за b
и a =
0, тогава стъпка 3 няма да може да се
изпълни заради не
възможността да се дели на 0. Процедурата не е алгоритмична, защото не
завършва успешно за някои стойности на входните
данни.
—На снимка към процедурата
от горния
слайд е добавена проверката дали a =
0. Тъй
като знакът за равенство вече
е запазен за присвояването на
стойност, сравняването на две
стойности за съвпадане означаваме с двойно равенство. Сега процедурата няма да спре
аварийно при a равно
на 0, но пък има друг дефект – ако a е
0 и b е 0,
тогава всяка стойност на x e решение, а процедурата ще изведе невярното съобщение "Няма
решение".
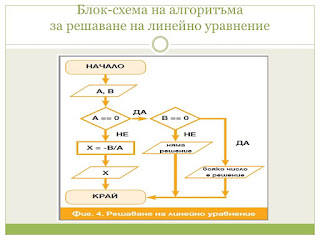
—С още една проверка, показана на втората
снимка като стъпка
6, поправяме и този дефект, за да получим
алгоритъма за решаване на
линейни уравнения.
Основни типове блокове
—1. Блокове за начало
и край (Фиг.
3а). Тези два блока са с овална форма. Блокът НАЧАЛО определя мястото, от което започва изпълнението на алгоритъма и се среща еднократно в блок-схемата.
В него не влизат стрелки и излиза една стрелка, показваща
кой е следващият блок. Блокът КРАЙ определя място,
където се прекратява изпълнението на алгоритъма. Такива блокове могат да бъдат няколко, като трябва да
има поне един. От него не излиза стрелка, а може да
влизат няколко.
2.
Блокове за вход и изход (Фиг. 3б). В първия вид блок се описват входни данни и се указва
моментът, в който алгоритъмът получава тези входни
данни. Вторият вид блок посочва момента на
извеждането и извежданите
междинни или крайни резултати. Произволен брой стрелки влизат и точно една стрелка
излиза от тези два вида блокове. Алгоритъмът изпълнява
предписаният вход или изход и продължава изпълнението
с блока, който е посочен от излизащата стрелка.
3.
Обработващият
блок (Фиг.
3в) има форма на правоъгълник и в
него се описват операции над обекти,
които не са проверки, например
изчисляване на изрази и
запазване на резултата. Произволен брой
стрелки влизат в този блок и точно една стрелка
излиза от него.
4. С блока от Фиг.
3г се предписва проверка
на
някакво условие. В резултат процедурата се разклонява на две в зависимост от това изпълнено
ли е условието или не. Блокът има произволен брой
входни стрелки и
две изходни. Ако условието е в сила,
изпълнението продължава
с блока, към който сочи стрелката, надписана с ДA, а ако не – с блока, към който
сочи стрелката, надписана с НE.
Блок-схема на алгоритъма
за решаване на линейно уравнение
за решаване на линейно уравнение